 |
 |
 |
 |
 |
 |
|
|
|
|
|
|
9. CampionamentoOBIETTIVO:
analizzare i caratteri del campione e spiegare perché non esiste il «campione perfetto»
È intuitivo che da una popolazione possono essere estratti moltissimi campioni, che probabilmente saranno tutti diversi fra loro:
È altrettanto intuitivo che le caratteristiche di un campione non saranno mai perfettamente identiche a quelle della popolazione. Il campione non sarà mai la «fotocopia» precisa della popolazione di origine. Quindi, se studi un campione allo scopo di effettuare una inferenza sulla popolazione, giungerai inevitabilmente a conclusioni non del tutto veritiere. In questa unità, e nelle successive, imparerai come ovviare a questo inconveniente.
Immagina di aver effettuato una 
indagine su un campione; in pratica, hai misurato un certo carattere in ciascuna delle unità del campione. Ora vuoi utilizzare i tuoi dati per trarre delle conclusioni. Ti devi porre due domande fondamentali:
La risposta a queste due domande genera i concetti di validità interna e di validità esterna di uno studio epidemiologico eseguito su un campione (studio campionario).
La validità interna misura quanto i risultati di uno studio sono corretti per il campione di individui che sono stati studiati. Essa viene detta «interna» perché si applica al campione, e non necessariamente agli altri individui della popolazione. Forse questo concetto ti potrà sembrare una sottigliezza inutile. Però devi pensare che non sempre si tratta di fare misurazioni facili, semplici e affidabili (come ad esempio pesare ratti da laboratorio). In molti casi, le cose sono più complicate: negli studi clinici, la validità interna dipende dalla correttezza di impostazione dello studio stesso, dalla scelta di buone tecniche diagnostiche e da un loro corretto utilizzo, da una buona elaborazione dei dati ecc. Nel caso dei dati ottenuti attraverso questionari, un fattore che contribuisce ad abbassare la validità interna è rappresentato dalla propensione degli intervistati a mentire sistematicamente su determinate domande, come illustrato nell'esempio che segue.
ESEMPIO. Effettui un sondaggio per conoscere la percentuale di cani che vengono sottoposti a vaccinazione periodica nei confronti della leptospirosi; a questo scopo, sottoponi ai proprietari dei cani la seguente domanda: «Lei fa vaccinare annualmente il suo cane per la leptospirosi?».
Prevedibilmente i proprietari che hanno cura del loro cane (e che lo vaccinano regolarmente) saranno ben felici di rivelare il loro comportamento virtuoso e quindi risponderanno correttamente con un "sì". Al contrario, molti di coloro che omettono di vaccinare il cane non saranno disposti ad ammetterlo, per non apparire egoisti o avari, e quindi tenderanno a mentire, rispondendo anch'essi con un "sì". Ciò evidentemente farà diminuire la validità interna del campione.
La validità interna viene diminuita sia dalla 
variazione casuale che da ogni elemento di bias. La validità interna è condizione necessaria ma non sufficiente perché uno studio sia utile.
La validità esterna è il grado di «generalizzabilità» delle conclusioni tratte da uno studio. Ad esempio, nel caso di uno studio epidemiologico clinico, essa risponde alla domanda "Supponendo che i risultati dello studio siano veri, essi si applicano anche ai miei pazienti?". In altre parole, la validità esterna misura il grado di verità dell'assunto secondo cui gli animali studiati sono "uguali" ad altri animali affetti dalla stessa condizione.
Per semplicità, assumiamo ora che lo studio sia provvisto di ottima validità interna; ciò significa che conosciamo con esattezza le caratteristiche del campione che abbiamo esaminato. Le conclusioni che ne abbiamo tratto sono certamente valide per gli individui del campione, ma non possiamo dire se e quanto tali conclusioni siano generalizzabili alla popolazione da cui il campione è stato estratto. La soluzione a questo problema verrà accennata nelle unità successive ( metodi di campionamento, limiti fiduciali, ecc.).
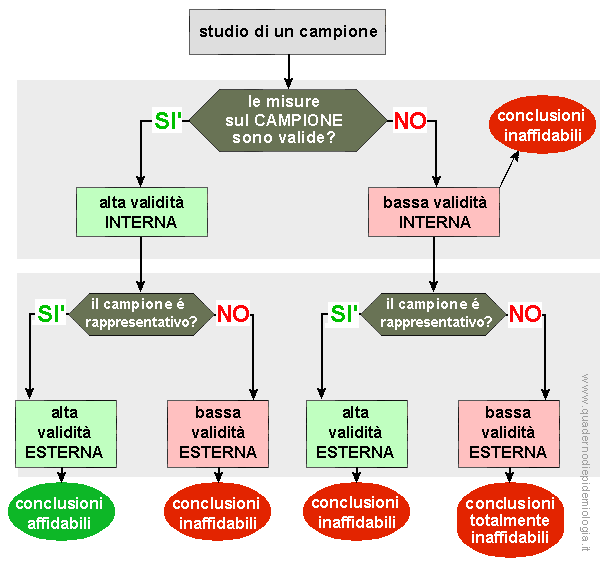
Ovviamente, le conclusioni ottenute attraverso uno studio campionario sono valide soltanto se esiste una buona validità interna ed esterna. Nella figura seguente viene schematizzato il flusso del ragionamento riguardo alla validità interna ed esterna di un campione, al fine di giungere a conclusioni affidabili.
È intuitivo che::
accuratezza della stima è direttamente correlata al numero di osservazioni che si compiono del fenomeno in studio.
ESEMPIO 1. Vogliamo conoscere il peso di un gruppo di 600 suini pronti per la macellazione. Non abbiamo la possibilità di pesare tutti i 600 animali; quindi, estraiamo un campione di 6 soggetti, li pesiamo e calcoliamo la media. È evidente che, con questo metodo, avremo un valore che si potrà scostare anche di parecchi chili dalla media della 'popolazione' da cui essi provengono (cioè il gruppo di 600). Ma se misuriamo altri individui e li aggiungiamo ai primi, la nuova media ottenuta sarà più vicina a quella vera; cioè, la precisione della nostra misura aumenterà parallelamente all'aumento del numero di animali pesati. Tuttavia, non otterremo una misura perfetta finché non avremo pesato tutti i suini.
ESEMPIO 2. Abbiamo il compito di effettuare un'indagine sui rapporti fra mastite della bovina e produzione di latte. Nel territorio sono presenti, in pianura, 14 grandi allevamenti, per un totale di 2900 bovine adulte da latte; nella zona montagnosa, vi sono invece 36 piccoli allevamenti (300 animali in totale). La popolazione di interesse è: tutte le bovine da latte. L' unità di analisi è la singola bovina da latte. Le nostre risorse ci consentono di esaminare un campione di 300 animali. Se tutti gli animali verranno selezionati dagli allevamenti della pianura, avremo un campione non rappresentativo. Un campione più rappresentativo sarà invece rappresentato dal 90% circa di bovine degli allevamenti di pianura e dal 10% di vacche di montagna.
In sostanza, con qualunque metodo si effettui il campionamento, si otterranno dal campione dei risultati che quasi certamente si discostano (poco o tanto) dalla «vera» misura della popolazione. È ben vero che il campione dovrebbe rappresentare una immagine della popolazione ridotta dal punto di vista numerico ma fedele dal punto di vista qualitativo. Tuttavia, non possiamo mai essere sicuri che il campione rappresenti una copia perfetta della popolazione da cui esso è stato estratto, a meno di non esaminare... l'intera popolazione!
Infatti, posto [n=numero di individui che compongono una popolazione], supponiamo di analizzare il più ampio campione possibile costituito da [n-1] individui. Ebbene, è intuitivo che, anche in questo caso, il campione non sarà perfettamente rappresentativo della popolazione, in quanto l'unico individuo non esaminato potrebbe possedere caratteri molto diversi da quelli di tutti gli altri [n-1] individui.
L'errore di campionamento è rappresentato dalla differenza tra i risultati ottenuti dal campione e la vera caratteristica della popolazione che vogliamo stimare.
L'errore di campionamento non può mai essere determinato con esattezza, in quanto la «vera» caratteristica della popolazione è (e resterà!) ignota. Esso tuttavia può essere contenuto entro limiti più o meno ristretti adottando appropriati metodi di campionamento. Inoltre, esso può essere stimato; ciò significa che, con adatti metodi statistici, si possono determinare i limiti probabili della sua entità.
AFTER HOURS: Risposte sincere a domande imbarazzanti
NELLA PROSSIMA UNITÀ:
si prendono in considerazione i fattori che contribuiscono all'errore di campionamento; si parla anche della selezione viziata e dell'effetto del caso.
