Versione Mobile | Vai alla versione Desktop
Differenze tra versione Mobile e versione Desktop
OBIETTIVO:
apprendere come verificare l'esistenza di una correlazione fra due variabili; in particolare, apprendere la base del procedimento logico, ed un metodo statistico idoneo.
Finora, nello studio delle cause di malattia e del rischio, abbiamo preso in considerazione esempi con dati qualitativi. Infatti, abbiamo classificato gli animali in 4 categorie in base alla qualità del loro stato (ossia: malati/non malati) ed in base alla qualità dell'esposizione ad una presunta causa di malattia (ossia: esposti/non esposti), secondo una tabella 2x2 che ormai dovrebbe essere ben nota (v. sotto). Forse è utile ripetere che le 4 categorie sono rappresentate da animali (a) esposti e ammalati; (b) esposti e non ammalati; (c) non esposti e ammalati; (d) non esposti e non ammalati.
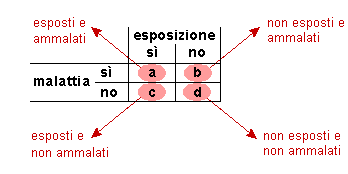
In molti casi, un tale approccio strettamente "qualitativo" rappresenta una limitazione dei dati ottenibili in studi epidemiologici sulle cause di malattia. Basti pensare che, in molti casi, la classificazione di un animale nella categoria "esposti" o in quella "non esposti" è in larga misura arbitraria e rappresenta, in una certa misura, una forzatura della realtà.
Ad esempio, animali che hanno avuto un'unica, lieve e transitoria esposizione ad una presunta causa potrebbero essere (indebitamente?) classificati come "esposti" ed essere assimilati ad altri animali che, invece, hanno subìto una esposizione intensa e prolungata nel tempo. Insomma: spesso l'esposizione non è un fenomeno tutto-o-niente, ma avviene secondo un gradiente misurabile.
Anche la classificazione nelle due classi "malati" e "non malati" talvolta non è soddisfacente, in quanto la stessa malattia può manifestarsi con gravità molto variabile e con segni clinici misurabili e rappresentabili numericamente.
Per riassumere: ci sono casi in cui sia l'esposizione che la malattia si misurano quantitativamente, e tali misure sono esprimibili attraverso numeri.
ESEMPIO. Una partita di mangime è contaminata da un fungo che produce una potente tossina (micotossina) che provoca emolisi (distruzione dei globuli rossi), e quindi anemia. L'intensità della esposizione potrebbe essere misurata attraverso la dose di micotossina ingerita/giorno; la gravità della malattia essere misurata potrebbe essere misurata attraverso il conteggio degli eritrociti nel sangue.
Ecco quindi sorgere la necessità di disporre di altri metodi di studio, diversi dalla "solita" tabella 2 x 2, per verificare l'esistenza di un rapporto causa-effetto quando i dati sono quantitativi.
Per rafforzare quanto finora esposto, ti ricordo che - sempre riguardo alla dimostrazione della causalità - hai già imparato un principio generale abbastanza intuitivo: "se fra fattore ed una malattia si individua una correlazione dose-effetto, allora quel fattore può essere una delle cause della malattia" (
regole di John Stuart Mill). Infatti, è ragionevole pensare che quanto più intensa è la causa, tanto più grave (o frequente) sarà la malattia. Analogamente, uno dei cinque criteri di causalità afferma che la forza di una associazione aumenta se si dimostra l'esistenza di una correlazione dose-effetto. È evidente che quando si parla di «correlazione dose-effetto« si parla di dati quantitativi, per i quali è necessario un approccio diverso da quello che hai imparato finora.
In questa Unità, attraverso un esempio, esaminerai uno dei metodi più usati come per studiare e descrivere una relazione quantitativa tra due variabili: la regressione lineare.
La regressione lineare serve per descrivere la relazione tra due variabili quantitative
Supponiamo di sospettare che, fra gli effetti indesiderati di un certo farmaco, si annoveri quello di innalzare la pressione arteriosa.
Verifichiamo questa ipotesi attraverso un esperimento: somministriamo dosi crescenti del farmaco ad alcuni ratti da esperimento, e misuriamo la variazione della pressione diastolica che si verifica dopo la somministrazione.
In dettaglio, vengono utilizzati 16 ratti, suddivisi in 8 gruppi di 2 animali ciascuno. Il primo gruppo è di controllo e non viene trattato; al secondo gruppo il farmaco viene somministrato in dose di 1 mg/kg, al terzo gruppo in dose di 2 mg/kg e così via. I risultati sono riassunti nella seguente tabella.
Osserva bene i dati della tabella: anche "a occhio" si nota che la variabile dipendente (ossia l'effetto: innalzamento della pressione) è correlata alla variabile indipendente (ossia la presunta causa: il farmaco). In altre parole: l'entità dell'aumento della pressione sembra essere associata alla dose.
Esiste un modo per visualizzare graficamente l'andamento del fenomeno: basta utilizzare i dati delle due variabili per costruire un diagramma a nuvola di punti (detto anche diagramma a dispersione, o diagramma xy; in inglese: scatterplot): in un sistema di assi cartesiani si pone: asse x=variabile indipendente e asse y=variabile dipendente. Con i dati dell'esempio, sull'asse x poniamo il farmaco e sull'asse y la variazione della pressione, ottenendo il seguente diagramma:
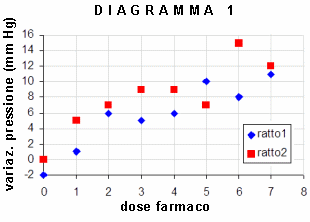
Per interpretare un diagramma a dispersione occorre valutarne l'aspetto globale, che rivela (1) la direzione, (2) la forma e (3) la forza della relazione che lega le due variabili. Vediamo brevemente queste tre caratteristiche.
DIREZIONE. L'aspetto del Diagramma 1 dimostra l'esistenza di una associazione positiva. Infatti, due variabili (ti ricordo che nell'esempio le variabili sono: x= la dose del farmaco, y= l'aumento della pressione) si dicono associate positivamente quando i valori alti di una variabile tendono a presentarsi insieme ai valori alti dell'altra variabile, ed analogamente i valori bassi dell'una tendono a presentarsi insieme ai valori bassi dell'altra. Viceversa, due variabili sono associate negativamente quando ai valori alti dell'una tendono ad associarsi valori bassi dell'altra variabile. Nei casi in cui le variabili non sono associate, la direzione non può essere individuata.
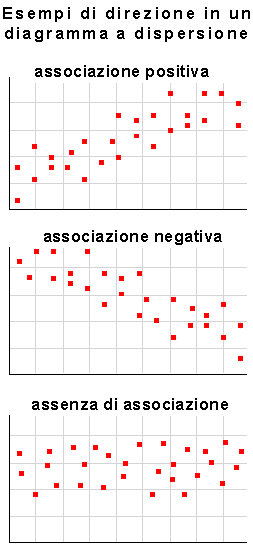
FORMA. La forma viene desunta dalla disposizione dei punti nel diagramma. Parleremo soltanto della regressione lineare, ossia del caso in cui i punti si dispongono approssimativamente su una linea retta. Esistono anche altri tipi di relazioni, non lineari e quindi più complesse, ma le relazioni lineari sono particolarmente importanti per un buon motivo: la linea retta è quella su cui tende a disporsi molto frequentemente il "pattern" dei punti ottenuti in molti studi biologici.
FORZA. La forza si può desumere dal grado di disseminazione dei punti nel diagramma. Se i punti sono molto disseminati, (ma sempre con tendenza a disporsi su una retta), la relazione tra le due variabili è debole; se invece i punti sono raggruppati attorno ad una retta, allora la relazione è forte. Anche l'inclinazione della retta è importante: tanto più la retta è inclinata, quanto più la relazione è forte.
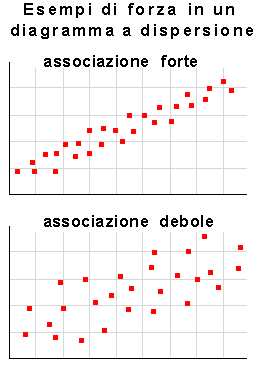
Esiste un metodo per formalizzare direzione, forma e forza di una relazione lineare fra due variabili. Questo metodo viene trattato nella prossima Unità.
NELLA PROSSIMA UNITÀ:
si continua a parlare di regressione, ed in particolare viene mostrato come riassumere con un numero (il coefficiente di correlazione) e con una retta (la retta di regressione) quanto imparato in questa unità didattica.
