Versione Mobile | Vai alla versione Desktop
Differenze tra versione Mobile e versione Desktop
OBIETTIVO:
imparare l'utilizzo del test t attraverso un esempio
Nella 
unità precedente hai imparato come stabilire (attraverso il test del chi-quadrato) se due proporzioni (o due percentuali) sono significativamente diverse fra loro.
Vi sono molte altre situazioni in cui devi risolvere un problema concettualmente simile: quello di confrontare due (o più) valori ottenuti studiando due (o più) gruppi, ma avendo a disposizione, invece di due percentuali, dati di altro tipo. Ad esempio, potresti confrontare una variabile qualitativa con una variabile quantitativa, oppure una qualitativa con un'altra pure qualitativa, o ancora più variabili quantitative con una o più variabili numeriche ecc. ecc. Ciascuno di questi casi richiede un test statistico adatto.
In effetti, uno degli aspetti più difficili (...per i non-statistici!) nell'elaborazione dei dati consiste proprio nella scelta del test da utilizzare: c'è anche chi ha paragonato la statistica... all'arte culinaria: un test statistico è come una ricetta di cucina. Un buon cuoco ottiene un buon piatto a partire dagli ingredienti che ha a disposizione, così come uno studioso ottiene informazioni veritiere «cucinando» opportunamente, con un test statistico adatto, i dati che ha raccolto.
UN PROBLEMA FREQUENTE: CONFRONTARE DUE MEDIE
Una circostanza frequente è quella in cui si sono esaminati due (o più) campioni di animali; sugli animali di ciascun campione è stata misurata una variabile numerica (es. altezza, peso, frequenza cardiaca, produzione di latte ecc.), di cui è stata poi calcolata la media.
Ti chiedi: la differenza fra le medie dei due campioni è significativa?
Ossia: puoi affermare che la differenza osservata non è dovuta al caso ma che, invece, esiste veramente una diversità tra le medie delle due popolazioni da cui i campioni stessi derivano? Oppure, esprimendoci in altro modo: puoi affermare che i due campioni appartengono a popolazioni diverse riguardo alla variabile considerata?
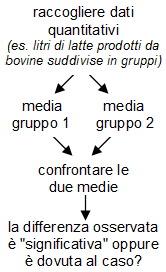
Come vedi la questione, in buona sostanza, è analoga a quella della unità precedente in cui hai utilizzato il test del chi-quadrato per confrontare due proporzioni. Il fatto è che la «ricetta» del chi-quadrato va bene per confrontare due proporzioni, ma non è utilizzabile se devi confrontare due medie. Allora, devi ricorrere a un altro test: ad esempio il test «t» (detto anche t di Student).
Lo schema di ragionamento da fare è quello già visto:
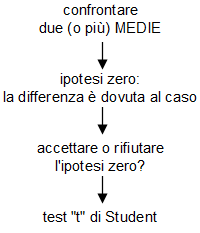
I calcoli da eseguire per effettuare il test t sono un po' più complicati rispetto a quelli del chi-quadrato, e perciò non entreremo nei dettagli. Solo a titolo di curiosità, ecco la formula di calcolo del valore t:
... e per i più interessati (o masochisti?) dirò che s è la deviazione standard media delle deviazioni standard dei due campioni, cioè la radice quadrata della varianza che si ottiene sommando le devianze dei due campioni e dividendo per la somma dei gradi di libertà.
Una volta trovato il valore t, esso va confrontato con quelli tabulati in apposite Tabelle, che si trovano in tutti i libri di statistica. Dal confronto fra il valore ottenuto e quello tabulato si potrà stabilire se la differenza fra le due medie è dovuta al caso o no.
Ora che ti ho esposto brevemente il principio che "sta dietro" al calcolo del test t di Student, ti consiglio di non preoccuparti più di tanto di calcoli e tabelle di raffronto (che, fra l'altro, sono più complesse di quanti ti aspetteresti, vedi un esempio qui). Oggi, infatti, il test t si esegue al computer con l'aiuto di apposito software, incluso in pacchetti statistici oppure reperibile in rete. Ad esempio, alla fine di questa unità troverai un foglio di calcolo con cui calcolare il valore t su una serie di dati che tu stesso puoi inserire.
In conclusione: è importante che tu conosca non tanto il metodo di calcolo (difficile da ricordare), quanto l'esistenza del test t e il contesto in cui esso si applica. Ancora più importante è che tu sia convinto che, anche nel confronto fra due medie, non si possono trarre conclusioni soggettive «ad occhio», ma è indispensabile ricorrere a un test statistico.
Stai sperimentando l'effetto sul suino dell'aggiunta alla razione di una miscela «probiotica» costituita da batteri normalmente presenti nella flora intestinale del suino. L'ipotesi da verificare è che il probiotico favorisca l'accrescimento degli animali.
Allo scopo di verificare l'ipotesi, hai disegnato uno studio sperimentale preliminare su due piccoli gruppi di suini. I gruppi sono fra loro omogenei (stessa razza, età, provenienza ecc.) e sono mantenuti nelle stesse condizioni di allevamento (alimentazione, temperatura ambiente ecc.). L'unica differenza è che alla razione del Gruppo 1 (10 suini) viene aggiunto il probiotico, mentre al gruppo 2 (11 suini) no.
All'inizio dell'esperimento ciascun suino viene pesato; dopo 21 giorni di trattamento i suini vengono pesati di nuovo e per ogni animale si calcola l'incremento giornaliero medio. I dati (fittizi) sono riportati nella tabella che segue.
Confrontando le medie degli accrescimenti, puoi notare che il valore del Gruppo 1 è superiore a quello del Gruppo 2 (643.8 g/giorno contro 637.0 g/giorno). La domanda è: questa differenza è dovuta al probiotico oppure al caso?
L'ipotesi zero dice che la differenza è dovuta al caso... accetti o rifiuti questa ipotesi? Per rispondere, puoi applicare ai tuoi dati il test t.
Tieni presente, però, che il test t va bene soltanto se i dati hanno una distribuzione Normale (se ti serve un rapido ripasso di questo argomento, dai un'occhiata al 
Cap. 7). La trattazione dei metodi per verificare la Normalità di un set di dati va oltre gli scopi del Quaderno. In linea di massima, si utilizza un software statistico (tutti i pacchetti statistici hanno funzioni adatte a questo scopo). In Excel, si possono utilizzare le formule ASIMMETRIA e CURTOSI.
I dati dell'esempio, sottoposti ad analisi, risultano avere una distribuzione normale.
Infine, per i più interessati, aggiungo che, se i dati non hanno una distribuzione normale, è necessario normalizzarli (con metodi sui quali non mi dilungo) oppure ricorrere a test diversi dal t di Student (es. il Test Mann-Whitney o il Test di Wilcoxon).
Una volta verificata la Normalità dei tuoi dati, puoi tranquillamente applicare il test t.
Ottieni un valore t pari a 2.2796.
Che farne, di questo valore? Il procedimento di base è abbastanza simile a quello che hai già appreso nel caso del test Chi-quadrato. In pratica, devi confrontare il valore t che hai ottenuto (2.2796) con quelli presenti nella Tabella dei valori t, per 19 gradi di libertà (gradi di libertà=numero osservazioni-numero gruppi; nel nostro esempio 21-2=19).
Il tuo valore è superiore a quello della colonna p=5% (ma inferiore a quello della colonna p=1%). Perciò puoi rifiutare l'ipotesi zero e concludere che la differenza è significativa per p<0.05 (ma non per p<0.01).
Ciò significa che c'è una probabilità inferiore al 5% (ma non all'1%) che la differenza di accrescimento tra il gruppo trattato e quello di controllo sia dovuta al caso.
Nota che i due valori p (0.05 e 0.01) sono valori convenzionalmente utilizzati nel modo scientifico (questo concetto viene spiegato meglio nella prossima unità).
Se hai utilizzato il mio foglio di calcolo (oppure un software statistico), il passaggio testé descritto (ossia quello di confrontare il tuo valore t con i valori della Tabella per 'n' gradi di libertà) è inutile: infatti il programma restituisce direttamente il valore p.
Con i tuoi dati ottieni: p=0.0344.
Ciò significa che c'è una probabilità inferiore a 3.44% che la differenza di accrescimento tra il gruppo trattato e quello di controllo sia dovuta al caso. In altri termini, puoi affermare che «la differenza fra gli animali trattati e i controlli è significativa per p=0.0344».
I risultati di un test statistico vanno interpretati correttamente. Vale la pena di ripetere qui quanto già detto nella Unità precedente a proposito del test del chi-quadrato: qualsiasi test di significatività non può mai provare con assoluta certezza che una ipotesi zero è vera o falsa; esso può solo fornire una indicazione della forza con cui i dati contrastano l'ipotesi zero.
Per consolidare quanto appreso in questa unità ti consiglio di leggere subito la successiva, che consolida i concetti di «livello di significatività» e di «ipotesi zero».
NELLA PROSSIMA UNITÀ:
si generalizza di quanto appreso in questa unità e in quella precedente. Infatti, vi si parla di un concetto generale come il «livello di significatività» di un test, si illustra l'approccio ai dati in base all'«ipotesi zero» e si elencano alcuni fra i test statistici più usati nella ricerca bio-medica.
